Consider the collection1 of all contiguous subsequences of a sequence. If we’re talking about a stream of n observations, this could be the multiset of windows containing every possible window over these observations: 1 window of n samples, 2 windows of n-1 samples, 3 windows of n-2 samples, …, and n “windows” of 1 sample each. If we’re talking about a string of symbols, e.g., abcde, then we’d be talking about the following set of substrings:
{
abcde,
abcd, bcde,
abc, bcd, cde,
ab, bc, cd, de,
a, b, c, d, e
}Given a sequence of n elements, there will be T(n) subsequences in such a collection, where T(n) is the nth triangular number. If we must store each subsequence without using some representation where two subsequences can share elements they have in common (e.g., if we were to store each as a distinct C-style array), the space requirements to do so explode quickly:
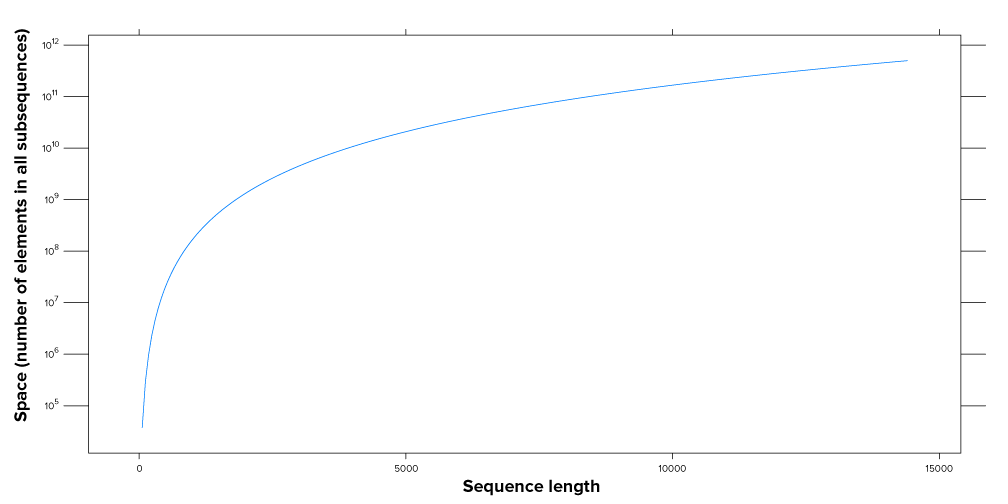
Anyway, I’m curious if this concept has a name. I’ve been thinking of it as a “power substring,” analogously to a powerset. If you know of a name for it, please let me know!
Footnotes
I find myself thinking of subsequence identity as depending upon its position in the parent sequence, and thus thinking of this collection as a set even if it could contain multiple subsequences with identical elements.↩︎